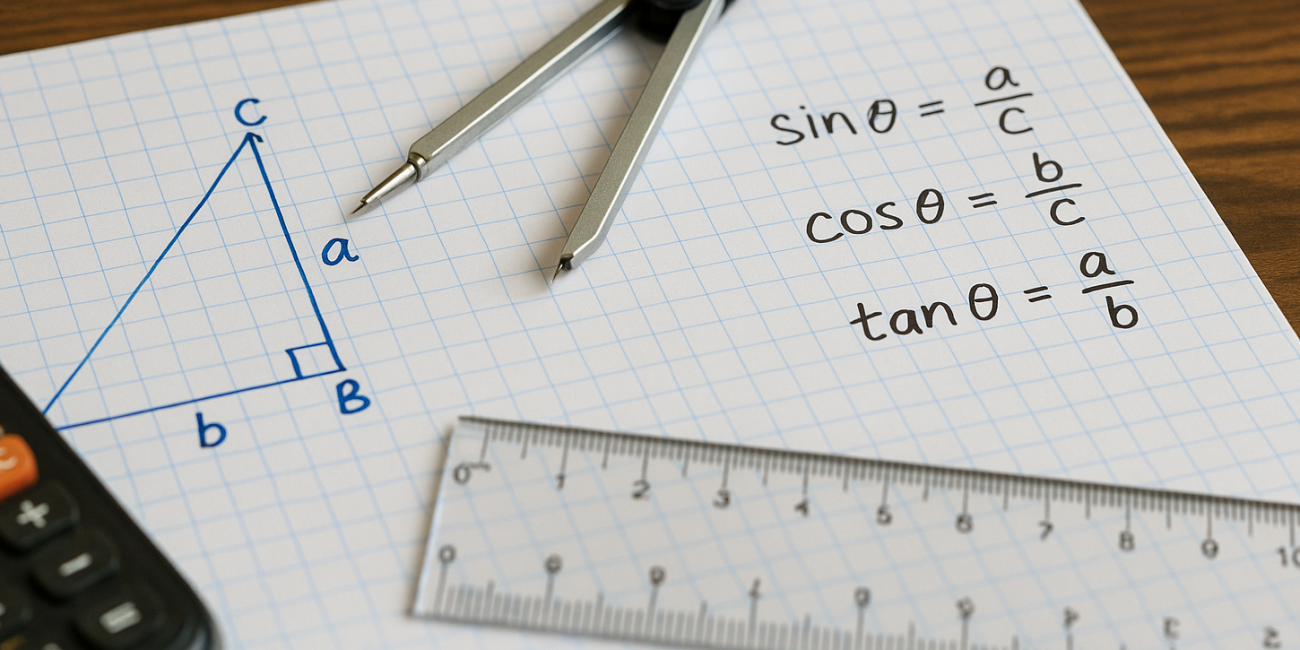Що таке синус, косинус і тангенс: простою мовою для школярів і дорослих

Синус, косинус і тангенс — це основні поняття в тригонометрії, які вивчаються ще в школі, зокрема в темі «гострого кута прямокутного трикутника 8 клас». Вони допомагають описувати співвідношення між сторонами трикутника і знаходити значення різних кутів. Але часто ці терміни викликають труднощі у розумінні. У цій статті ми детально й просто пояснимо, що це таке, як знайти значення для різних кутів і де вони застосовуються.

Основи тригонометрії: що означають синус, косинус і тангенс

Тригонометричні функції базуються на властивостях прямокутного трикутника. Кожна функція визначає співвідношення між певними сторонами відносно кута.

• Синус кута — це відношення протилежного катета до гіпотенузи.
• Косинус кута — це відношення прилеглого катета до гіпотенузи.
• Тангенс кута — це відношення протилежного катета до прилеглого катета.

Ці визначення актуальні для будь-якого гострого кута прямокутного трикутника.

Як знайти синус, косинус і тангенс кута

Щоб знайти значення синуса, косинуса чи тангенса, потрібно знати довжини сторін прямокутного трикутника. Розглянемо це на прикладі:

Нехай у прямокутному трикутнику гіпотенуза дорівнює 10 см, один катет (прилеглий) — 8 см, а другий (протилежний) — 6 см.

• Синус = протилежний катет / гіпотенуза = 6 / 10 = 0,6
• Косинус = прилеглий катет / гіпотенуза = 8 / 10 = 0,8
• Тангенс = протилежний / прилеглий = 6 / 8 = 0,75

Такі розрахунки використовуються на практиці під час побудов або розв’язування задач на кути.

Значення тригонометричних функцій для кутів від 0° до 180°

У шкільній програмі розглядаються значення синуса, косинуса і тангенса не лише для гострих, а й для розгорнутих кутів. Нижче подано кілька стандартних значень:

• sin 0° = 0, cos 0° = 1, tg 0° = 0
• sin 30° = 0,5, cos 30° ≈ 0,87, tg 30° ≈ 0,577
• sin 45° ≈ 0,707, cos 45° ≈ 0,707, tg 45° = 1
• sin 60° ≈ 0,87, cos 60° = 0,5, tg 60° ≈ 1,73
• sin 90° = 1, cos 90° = 0, tg 90° — не існує
• sin 180° = 0, cos 180° = -1, tg 180° = 0

Знання цих значень корисне для розв’язування задач у геометрії, фізиці та інженерії.

Де застосовуються синус, косинус і тангенс

Тригонометричні функції застосовуються не тільки в математиці, а й у багатьох практичних сферах:

• Будівництво та архітектура. Визначення висоти, нахилу, довжини.
• Фізика. Опис руху, коливань, сили.
• Інформатика. Побудова графіки, анімації, обробка зображень.
• Астрономія. Розрахунок траєкторій планет та супутників.
• Навігація. Визначення напрямку та відстаней.

Що потрібно знати учням 8 класу

У 8 класі особлива увага приділяється розумінню того, як знайти синус, косинус і тангенс гострого кута прямокутного трикутника. Учні мають вивчити:

• Формули для кожної функції
• Як знаходити сторони за відомим кутом і стороною
• Як використовувати калькулятор для обчислення значень
• Таблицю значень синуса, косинуса і тангенса для основних кутів

Це важливий етап, оскільки закладає фундамент для подальшого вивчення тригонометрії в старших класах.

Корисні поради для запам’ятовування

Ось кілька способів, які допоможуть легше засвоїти матеріал:

1. Мнемоніка. Наприклад, фраза «Соня Каже Танцюй» — скорочення від С=П/Г, К=Пл/Г, Т=П/Пл.
2. Візуалізація. Малюйте трикутники, позначайте кути та сторони — так легше зрозуміти співвідношення.
3. Тренування. Розв’язуйте приклади з підручників або онлайн-платформ.

Часті помилки і як їх уникнути

Учні часто плутають, яка сторона вважається прилеглою, а яка — протилежною. Варто пам’ятати:

• Протилежна — це та, що навпроти кута.
• Прилегла — та, що поруч із кутом, але не є гіпотенузою.
• Гіпотенуза — завжди навпроти прямого кута.

Також потрібно уникати округлення значень на ранніх етапах обчислення — це може вплинути на точність кінцевого результату.

Висновок

Синус, косинус і тангенс — це не просто складні слова, а важливі інструменти для опису геометричних і фізичних явищ. Вивчаючи, як знайти значення для кута від 0° до 180°, ми розширюємо свої можливості аналізу й побудови. Тригонометрія — це мова точності, і знання основ дозволяє краще розуміти світ, що нас оточує. Якщо з самого початку підійти до теми з інтересом, вона відкриється просто й доступно навіть для школярів.