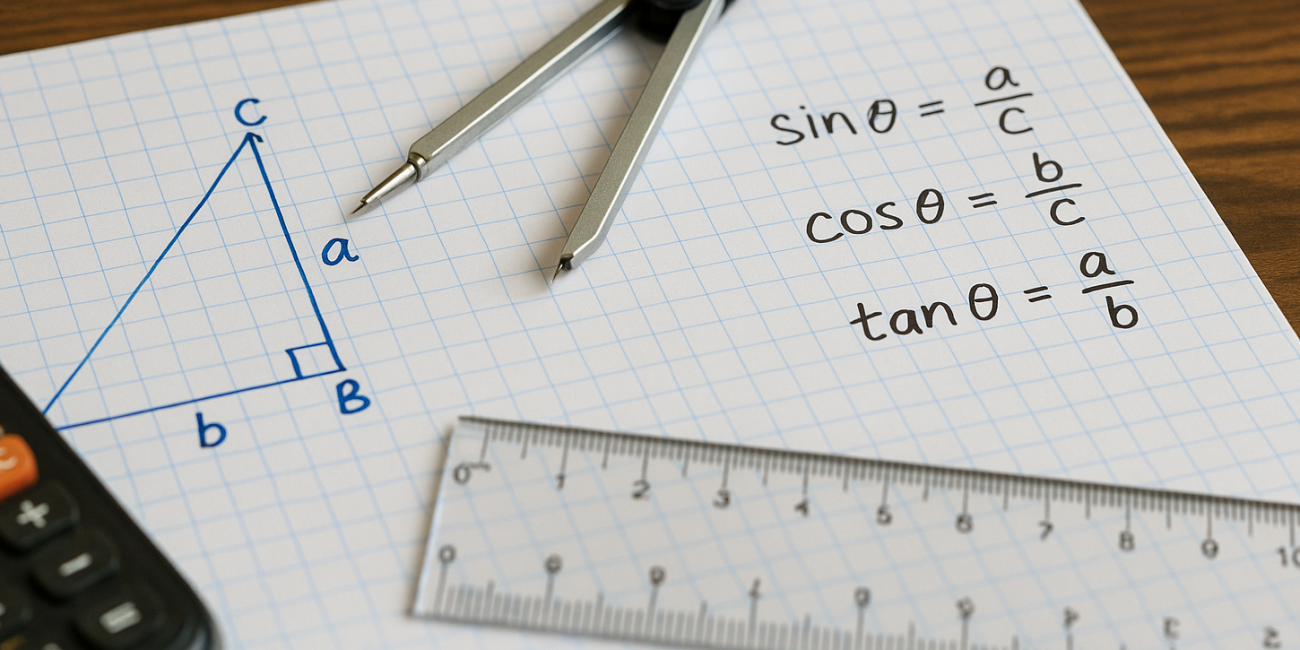Что такое синус, косинус и тангенс: простыми словами для школьников и взрослых

Синус, косинус и тангенс — это основные понятия в тригонометрии, которые изучаются ещё в школе, особенно в теме «острого угла прямоугольного треугольника 8 класс». Они помогают описывать соотношения между сторонами треугольника и находить значения различных углов. Однако часто эти термины вызывают трудности в понимании. В этой статье мы подробно и просто объясним, что это такое, как найти значения для разных углов и где они применяются.

Основы тригонометрии: что обозначают синус, косинус и тангенс

Тригонометрические функции основываются на свойствах прямоугольного треугольника. Каждая функция определяет отношение между определёнными сторонами относительно угла.

• Синус угла — это отношение противолежащего катета к гипотенузе.
• Косинус угла — это отношение прилежащего катета к гипотенузе.
• Тангенс угла — это отношение противолежащего катета к прилежащему катету.

Эти определения актуальны для любого острого угла прямоугольного треугольника.

Как найти синус, косинус и тангенс угла

Чтобы найти значение синуса, косинуса или тангенса, нужно знать длины сторон прямоугольного треугольника. Рассмотрим это на примере:

Пусть в прямоугольном треугольнике гипотенуза равна 10 см, один катет (прилежащий) — 8 см, а другой (противолежащий) — 6 см.

• Синус = противолежащий катет / гипотенуза = 6 / 10 = 0,6
• Косинус = прилежащий катет / гипотенуза = 8 / 10 = 0,8
• Тангенс = противолежащий / прилежащий = 6 / 8 = 0,75

Такие вычисления используются на практике при построениях или решении задач на углы.

Значения тригонометрических функций для углов от 0° до 180°

В школьной программе рассматриваются значения синуса, косинуса и тангенса не только для острых, но и для развёрнутых углов. Ниже приведены некоторые стандартные значения:

• sin 0° = 0, cos 0° = 1, tg 0° = 0
• sin 30° = 0,5, cos 30° ≈ 0,87, tg 30° ≈ 0,577
• sin 45° ≈ 0,707, cos 45° ≈ 0,707, tg 45° = 1
• sin 60° ≈ 0,87, cos 60° = 0,5, tg 60° ≈ 1,73
• sin 90° = 1, cos 90° = 0, tg 90° — не существует
• sin 180° = 0, cos 180° = -1, tg 180° = 0

Знание этих значений полезно при решении задач по геометрии, физике и инженерии.

Где применяются синус, косинус и тангенс

Тригонометрические функции применяются не только в математике, но и во многих практических сферах:

• Строительство и архитектура. Определение высоты, наклона, длины.
• Физика. Описание движения, колебаний, силы.
• Информатика. Построение графики, анимации, обработка изображений.
• Астрономия. Расчёт траекторий планет и спутников.
• Навигация. Определение направления и расстояний.

Что нужно знать ученикам 8 класса

В 8 классе особое внимание уделяется пониманию того, как найти синус, косинус и тангенс острого угла прямоугольного треугольника. Ученики должны выучить:

• Формулы для каждой функции
• Как находить стороны по известному углу и стороне
• Как пользоваться калькулятором для вычислений
• Таблицу значений синуса, косинуса и тангенса для основных углов

Это важный этап, поскольку он закладывает фундамент для дальнейшего изучения тригонометрии в старших классах.

Полезные советы для запоминания

Вот несколько способов, которые помогут легче усвоить материал:

1. Мнемоника. Например, фраза «Саша Против Гены, Катя Против Гены, Таня Против Кати» — сокращения от С=П/Г, К=Пл/Г, Т=П/Пл.
2. Визуализация. Рисуйте треугольники, отмечайте углы и стороны — так легче понять соотношения.
3. Тренировка. Решайте примеры из учебников или на онлайн-платформах.

Частые ошибки и как их избежать

Ученики часто путаются, какая сторона считается прилежащей, а какая — противоположной. Важно помнить:

• Противоположная — это та, что напротив угла.
• Прилежащая — та, что рядом с углом, но не гипотенуза.
• Гипотенуза — всегда напротив прямого угла.

Также не стоит округлять значения на ранних этапах расчёта — это может повлиять на точность результата.

Заключение

Синус, косинус и тангенс — это не просто сложные слова, а важные инструменты для описания геометрических и физических явлений. Изучая, как найти значения для углов от 0° до 180°, мы расширяем свои возможности анализа и построения. Тригонометрия — это язык точности, и знание основ позволяет лучше понимать окружающий нас мир. Если с самого начала подойти к теме с интересом, она откроется просто и доступно даже для школьников.